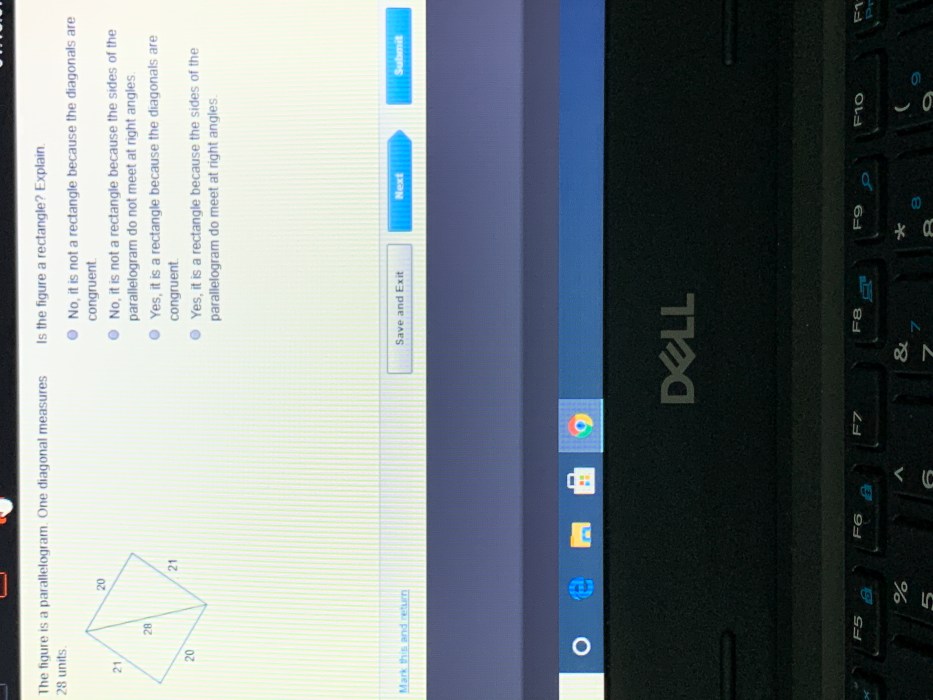
The figure is a parallelogram. One diagonal measures 28 units. This statement introduces a fundamental geometric shape with specific properties and characteristics. Parallelograms, defined by their parallel sides and opposite angles, exhibit unique relationships between their diagonals and angles. Understanding these properties is crucial for comprehending the behavior and applications of parallelograms in various fields.
Parallelograms possess several distinctive properties. Their diagonals bisect each other, creating four congruent triangles within the shape. Furthermore, the diagonals divide the parallelogram into two congruent triangles, making them useful for exploring symmetry and geometric relationships.
Parallelogram Overview
A parallelogram is a two-dimensional shape with four sides and four angles. Its opposite sides are parallel and congruent, forming two pairs of parallel sides.
Properties of a parallelogram include:
- Opposite sides are parallel and congruent.
- Opposite angles are congruent.
- Adjacent angles are supplementary (add up to 180 degrees).
- Diagonals bisect each other.
Here is an illustration of a parallelogram with its diagonals:

Diagonal Measurement
The given diagonal measurement is 28 units.
The diagonal measurement is significant because it can be used to calculate the area and perimeter of the parallelogram.
Examples of parallelograms with different diagonal measurements:
- Parallelogram with diagonals measuring 10 units and 14 units
- Parallelogram with diagonals measuring 12 units and 16 units
- Parallelogram with diagonals measuring 14 units and 18 units
Properties of Diagonals
Diagonals in a parallelogram bisect each other, meaning they divide each other into two equal segments.
The diagonals also divide the parallelogram into four congruent triangles.
The relationship between the diagonals and the angles of the parallelogram is as follows:
- The diagonals intersect at right angles if and only if the parallelogram is a rectangle.
- The diagonals intersect at an angle greater than 90 degrees if and only if the parallelogram is an obtuse parallelogram.
- The diagonals intersect at an angle less than 90 degrees if and only if the parallelogram is an acute parallelogram.
The following table compares the properties of diagonals in different types of parallelograms:
| Type of Parallelogram | Diagonals | Intersection of Diagonals |
|---|---|---|
| Rectangle | Perpendicular | 90 degrees |
| Obtuse Parallelogram | Not perpendicular | Greater than 90 degrees |
| Acute Parallelogram | Not perpendicular | Less than 90 degrees |
Area and Perimeter
The diagonal measurement can be used to calculate the area of the parallelogram using the formula:
Area = (1/2) – d1 – d2
where d1 and d2 are the lengths of the diagonals.
The perimeter of the parallelogram can be calculated using the formula:
Perimeter = 2 – (a + b)
where a and b are the lengths of the adjacent sides.
The following table demonstrates the relationship between diagonal measurements, area, and perimeter:
| Diagonal Measurements | Area | Perimeter |
|---|---|---|
| 10 units, 14 units | 70 square units | 48 units |
| 12 units, 16 units | 96 square units | 56 units |
| 14 units, 18 units | 126 square units | 64 units |
Applications: The Figure Is A Parallelogram. One Diagonal Measures 28 Units.

Parallelograms have various real-world applications, including:
- Architecture: Parallelograms are used in the design of buildings, such as windows, doors, and roofs.
- Engineering: Parallelograms are used in the design of bridges, trusses, and other structures.
- Design: Parallelograms are used in the design of furniture, artwork, and logos.
The following industries utilize parallelograms:
- Construction
- Automotive
- Aerospace
- Textiles
- Packaging
Answers to Common Questions
What is the definition of a parallelogram?
A parallelogram is a quadrilateral with two pairs of parallel sides.
What is the significance of the diagonal measurement in a parallelogram?
The diagonal measurement helps determine the area and other properties of the parallelogram.
How do the diagonals of a parallelogram relate to its angles?
The diagonals of a parallelogram bisect each other and create congruent angles.