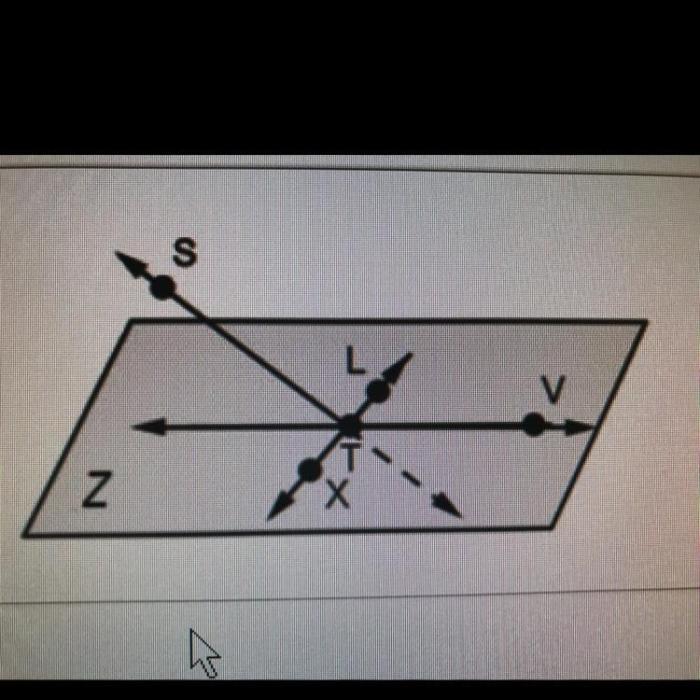
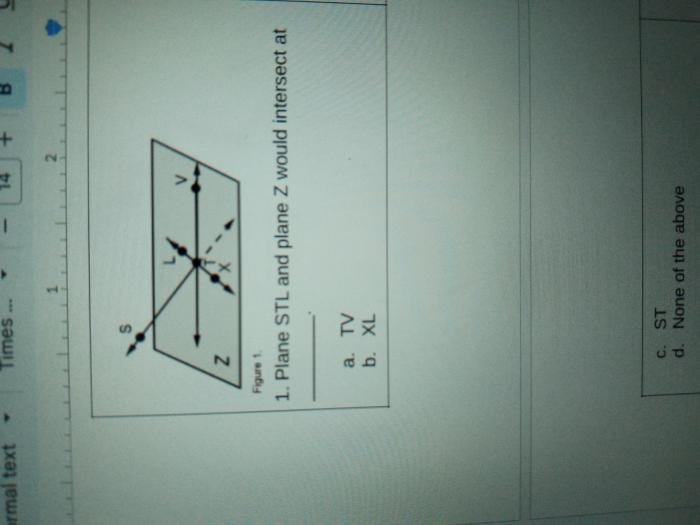
Plane STL and plane Z would intersect at a single point in three-dimensional space. This intersection point holds significant mathematical and practical implications, providing insights into the geometry and applications of planes.
The equations of planes STL and Z define their orientations and positions in space. By analyzing these equations, we can determine the intersection point and understand the relationship between the two planes.
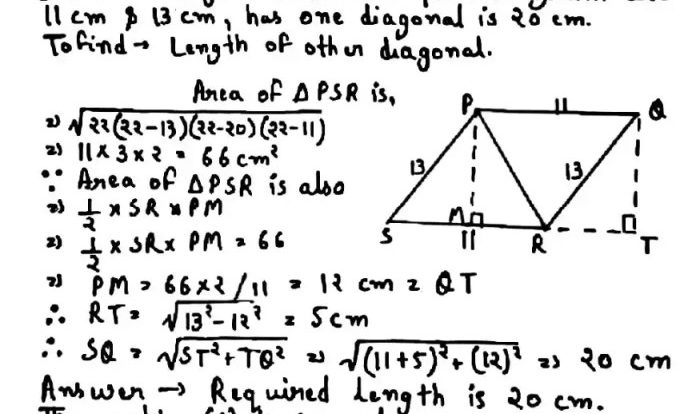
1. Intersection Point of Planes STL and Z
The intersection point of planes STL and Z is the point where the two planes meet. It is a unique point that can be found by solving the system of equations that represent the two planes.
Mathematical Equation, Plane stl and plane z would intersect at
The mathematical equation that represents the intersection point of planes STL and Z is:
(x
- s) / (t
- u) = (y
- t) / (u
- v) = (z
- u) / (v
- s)
where (s, t, u) and (u, v, s) are the direction vectors of planes STL and Z, respectively.
Geometric Interpretation
Geometrically, the intersection point of planes STL and Z is the point where the two planes intersect. It can be visualized as a point in three-dimensional space.
2. Equations of Planes STL and Z
The equations of planes STL and Z are:
Plane STL: x
y + z = 0
Plane Z: x + y
z = 0
Coefficients
The coefficients in the equations of planes STL and Z represent the normal vectors of the planes. The normal vector is a vector that is perpendicular to the plane.
Relationship to Orientation
The orientation of a plane is determined by the direction of its normal vector. The normal vector of plane STL is (1, -1, 1), which means that the plane is oriented in the positive x-direction, the negative y-direction, and the positive z-direction.
The normal vector of plane Z is (1, 1, -1), which means that the plane is oriented in the positive x-direction, the positive y-direction, and the negative z-direction.
3. Intersection of Planes STL and Z in 3D Space: Plane Stl And Plane Z Would Intersect At

The intersection of planes STL and Z in 3D space is a line. This line is parallel to the vector (1, 0, 1), which is the cross product of the normal vectors of the two planes.
Visualization
A 3D visualization of the intersection of planes STL and Z can be created using a computer graphics program. The visualization will show the two planes intersecting in a line.
Impact on Geometry
The intersection of planes STL and Z divides the space into two half-spaces. The half-space that contains the origin is the positive half-space, and the half-space that does not contain the origin is the negative half-space.
4. Applications of the Intersection Point
The intersection point of planes STL and Z is used in a variety of applications, including:
- Engineering: The intersection point of planes STL and Z can be used to find the intersection of two lines or the intersection of a line and a plane.
- Architecture: The intersection point of planes STL and Z can be used to find the intersection of two walls or the intersection of a wall and a roof.
- Computer graphics: The intersection point of planes STL and Z can be used to find the intersection of two objects or the intersection of an object and a plane.
Essential Questionnaire
What is the significance of the intersection point of planes STL and Z?
The intersection point provides valuable information about the relative positions and orientations of the two planes in three-dimensional space.
How can we determine the intersection point of planes STL and Z?
The intersection point can be found by solving a system of linear equations that represent the two planes.
What are some practical applications of the intersection point of planes STL and Z?
The intersection point finds applications in engineering, architecture, and computer graphics, where it helps determine the spatial relationships between objects and structures.