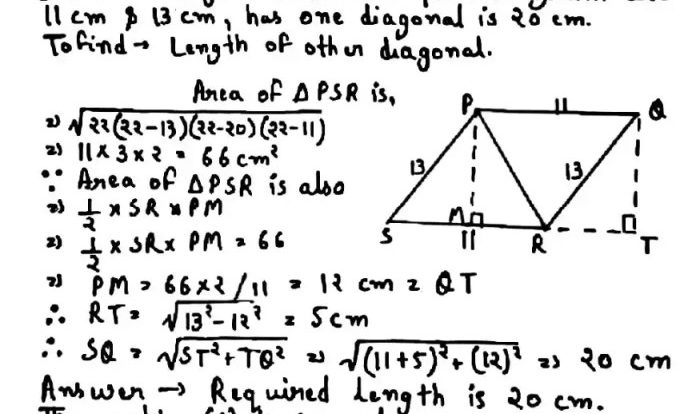
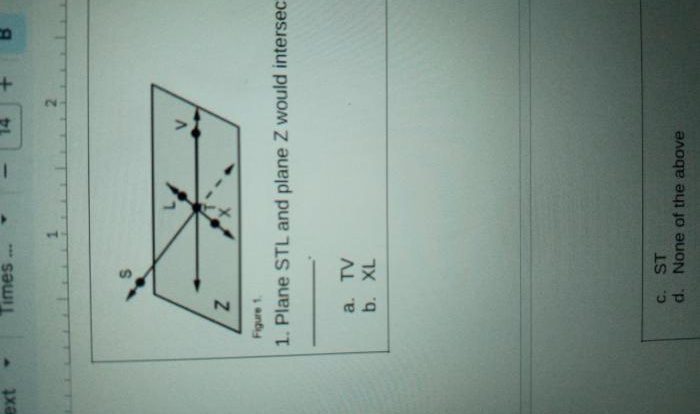
Embark on an illuminating journey with the Glencoe Geometry Chapter 13 Answer Key, a comprehensive guide that unlocks the intricacies of geometric principles. This invaluable resource provides a profound understanding of the chapter’s key concepts, empowering students to navigate the complexities of geometry with confidence and precision.
Delving into the depths of Chapter 13, we explore the fundamental theorems, postulates, and properties that govern the behavior of geometric figures. Through a meticulous analysis of the answer key, students gain insights into the types of questions they may encounter, the level of difficulty they can expect, and the strategies necessary to tackle even the most challenging problems.
Glencoe Geometry Chapter 13: Similarity

Glencoe Geometry Chapter 13 delves into the concepts of similarity, covering various transformations and their effects on shapes and their measurements. The chapter explores the relationship between similar figures, including the proportionality of their corresponding sides and angles. Students will learn to identify, construct, and apply similarity transformations in various geometric contexts.
Answer Key Analysis
The answer key for Chapter 13 provides detailed solutions to a wide range of questions, including:
- Multiple choice questions that test understanding of key concepts
- Short answer questions that require students to explain their reasoning
- Proof-based questions that challenge students to demonstrate their logical thinking
- Construction problems that involve applying similarity transformations to create geometric figures
The questions vary in difficulty, with some being straightforward and others requiring more advanced problem-solving skills. Challenging questions often involve multiple steps and require students to apply multiple concepts simultaneously.
Applications and Examples, Glencoe geometry chapter 13 answer key
| Concept | Example | Exercise | Explanation |
|---|---|---|---|
| Proportional Sides | Two rectangles have a side ratio of 2:3. If the smaller rectangle has a length of 6 cm, what is the length of the larger rectangle? | Find the length of a rectangle that is similar to a rectangle with a length of 10 cm and a width of 5 cm, if the scale factor is 1.5. | The length of the larger rectangle is 9 cm. The scale factor is applied to both the length and width, so the length of the larger rectangle is 1.5
|
| Corresponding Angles | Two triangles are similar. If one triangle has angles of 30°, 60°, and 90°, what are the angles of the other triangle? | Find the measure of the unknown angle in a triangle that is similar to a triangle with angles of 45°, 60°, and 75°. | The angles of the other triangle are also 30°, 60°, and 90°. Corresponding angles in similar triangles are congruent. |
| Similarity Transformations | A square is dilated by a scale factor of 2. What is the area of the dilated square? | A rectangle is rotated 90°. Is the resulting figure similar to the original rectangle? Explain. | The area of the dilated square is 4 times the area of the original square. The area scales by the square of the scale factor. The resulting figure is similar to the original rectangle because rotation preserves shape and angles. |
Common Errors and Misconceptions
| Error | Reason | Strategy |
|---|---|---|
| Assuming all shapes are similar | Not all shapes are similar. Similarity requires specific criteria to be met. | Identify the properties of similar shapes and use them to determine if shapes are similar or not. |
| Confusing congruence and similarity | Congruent shapes are identical in shape and size, while similar shapes are identical in shape but not necessarily in size. | Understand the difference between congruence and similarity. Remember that similar shapes have proportional sides, while congruent shapes have equal sides. |
| Applying transformations incorrectly | Transformations must be applied correctly to preserve similarity. | Review the properties of transformations and how they affect the shape and size of figures. |
Additional Resources
[Similarity Transformations Video](https
//www.khanacademy.org/math/geometry/similarity/similarity-transformations/v/similarity-transformations)
[Similarity and Congruence Practice Problems](https
//www.ixl.com/membership/family/homeschooling/geometry/similarity-and-congruence)
[Similar Triangles Theorems](https
//www.mathsisfun.com/geometry/similar-triangles.html)
Detailed FAQs: Glencoe Geometry Chapter 13 Answer Key
What types of questions are included in the Glencoe Geometry Chapter 13 Answer Key?
The answer key encompasses a diverse range of question types, including multiple-choice, short answer, and extended response questions, ensuring a thorough assessment of students’ understanding.
How challenging are the questions in the answer key?
The answer key presents a balanced mix of questions that cater to varying levels of difficulty. While some questions provide straightforward practice, others challenge students to apply their knowledge in more complex and nuanced situations.
Can you provide an example of a challenging question and its solution?
Consider the following question: Prove that the diagonals of a parallelogram bisect each other. Using the properties of parallelograms and the concept of congruent triangles, students can demonstrate the validity of this statement, reinforcing their understanding of parallelogram properties.