In the realm of mathematics, rules for sums of powers of integers stand as a cornerstone of understanding and calculation. These rules govern the behavior of expressions involving the repeated multiplication of integers by themselves, providing a framework for solving complex problems and unlocking insights into various phenomena.
From the fundamental concept of integer exponents to the practical applications in fields such as physics and engineering, this comprehensive guide delves into the intricacies of rules for sums of powers of integers, empowering readers with a deeper understanding of this essential mathematical concept.
Integer Exponents and Sums of Powers
Integer exponents are a way to represent repeated multiplication of a number by itself. For example, 2 3= 2 × 2 × 2 = 8. Sums of powers are expressions that involve adding up the powers of a number. For example, the sum of the first n integers is given by the formula 1 + 2 + 3 + … + n = n(n + 1)/2.
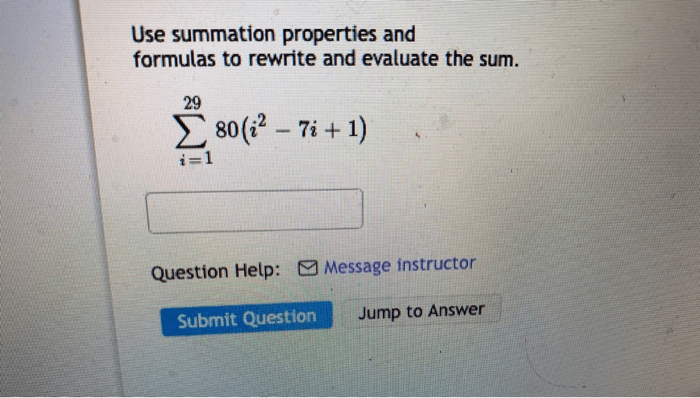
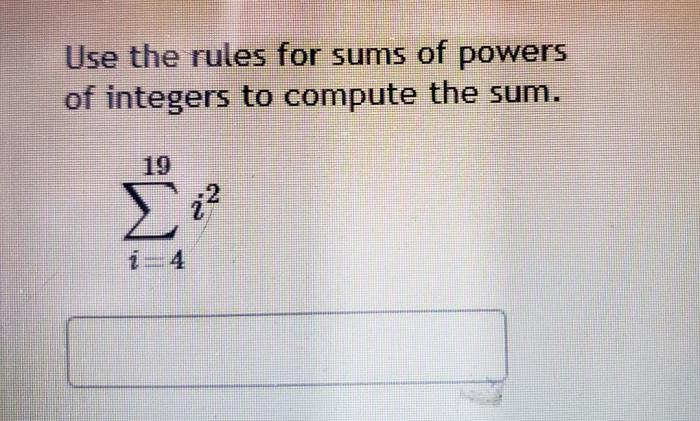
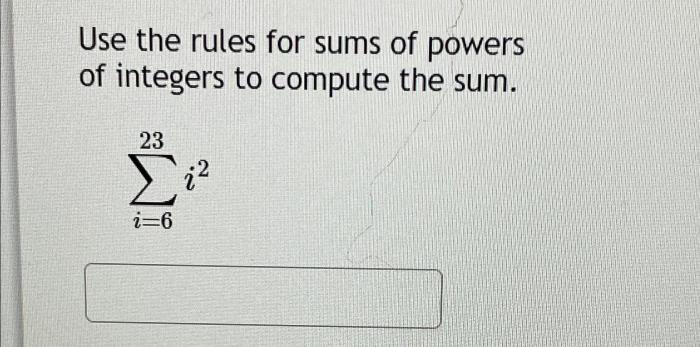
Sums of powers have many interesting properties. For example, the sum of the squares of the first n integers is given by the formula 1 2+ 2 2+ 3 2+ … + n 2= n(n + 1)(2n + 1)/6. The sum of the cubes of the first n integers is given by the formula 1 3+ 2 3+ 3 3+ … + n 3= n 2(n + 1) 2/4.
Summation Formulas for Powers of Integers, Rules for sums of powers of integers
- The sum of the first n integers is given by the formula 1 + 2 + 3 + … + n = n(n + 1)/2.
- The sum of the squares of the first n integers is given by the formula 1 2+ 2 2+ 3 2+ … + n 2= n(n + 1)(2n + 1)/6.
- The sum of the cubes of the first n integers is given by the formula 1 3+ 2 3+ 3 3+ … + n 3= n 2(n + 1) 2/4.
Applications of Summation Formulas
Summation formulas for powers of integers have many applications in real-world problems. For example, they can be used to calculate the area of a triangle, the volume of a sphere, and the center of mass of a distribution.
Generalizations and Extensions
The summation formulas for powers of integers can be generalized to other sequences of numbers. For example, the sum of the first n odd integers is given by the formula 1 + 3 + 5 + … + (2n – 1) = n 2. The sum of the first n even integers is given by the formula 2 + 4 + 6 + … + 2n = n(n + 1).
Quick FAQs: Rules For Sums Of Powers Of Integers
What is the significance of integer exponents in the context of sums of powers?
Integer exponents define the number of times an integer is multiplied by itself, providing a concise notation for repeated multiplication.
How do summation formulas for powers of integers facilitate calculations?
Summation formulas provide shortcuts for evaluating sums of powers of integers, reducing complex expressions to simpler forms.
What are some real-world applications of rules for sums of powers of integers?
These rules find applications in areas such as physics (calculating the center of mass), engineering (designing structures), and finance (modeling financial growth).